- TOP
- イノベーションのDNA
- 数理科学が暴いた!話題沸騰「ファインファイバー」の秘密
イノベーションのDNA

-
#数理科学 #創る/シミュレーション #不織布 #ファインファイバー
【特集:数理科学】
数理科学が暴いた!話題沸騰「ファインファイバー」の秘密
無限の化学に「本質の数理」が挑む(2)
-
2020/08/12 Text by 堀川晃菜

前回の記事では、日用品の開発における数理科学の応用として、「めぐりズム」の発熱シートや、ハンドソープの「キャラクター泡」の事例を紹介した。そして、今回紹介するのが最新技術「ファインファイバー」との接点だ。
これらはいずれも、まず現象が先にあり、その本質を理解することで、材料の物性や装置の構造を最適設計し、実験や開発の指針を提言することに数理科学の大きな役割がある。だが、数理科学の研究員が頭を抱えることもある。常識的にありえないはずのことが、現に目の前で起こっているときだ。ファインファイバーのその細さもまた、不可解なまでに細かったのだ。
“ありえない細さ” のファインファイバー
2018年、花王が発表したある1本の動画が巷をざわつかせた。そこに映るのは、見たこともない光景だった。
花王 Fine Fiber技術 Kao Fine Fiber Technology
手のひらに収まる小型デバイスから吐出される直径サブミクロン(1μm(マイクロメートル)未満)の極細繊維が、肌の表面でまたたく間に重なり合って「極薄膜」をつくっていく。まるで肌と見分けがつかないほど、透明で薄く、しなやかなその膜は“未来の肌”とも呼ばれている。
この「Fine Fiber Technology」(以降、ファインファイバー)は、早くも2019年にスキンケア製品への応用が実現し、今後は医療方面も視野に入れた展開が期待される注目の技術だ。
(ファインファイバーの開発経緯や応用事例については、こちら)。
それにしても、一体なぜ、ここまで細い繊維になるのか。サブミクロンともなると、髪の毛(50-80μm)の100分の1の細さになる。驚異的なレベルだ。
「デバイスのノズルは直径0.3ミリ(300㎛)です。ここから吐出した繊維が、直径1㎛未満になるということは、太さを300分の1に絞り込むことになります。溶媒の蒸発を考えないとして、これを長さに換算すると、9万倍に引き伸ばされることになります(延伸比は 300の2乗)。そして、ノズルからは典型値として 1秒間に3cm(毎秒0.03 m)の速さで吐出されるので、もしそのまま真っすぐ伸びるとすれば、速度は毎秒2700 mに達する計算になります。これでは音速(25℃で毎秒346m)をはるかに上回ってしまいます」
(音速を超える……?) 花王 加工・プロセス開発研究所の成島毅氏の解説に、頭がフリーズしそうになるが、気を取り直して、先ほどの動画を振り返ってみる。

-
図1. 小型デバイスから吐出されたファインファイバーの様子。
よく見ると、ノズルから吹き出された繊維は、しばらく直進したのち、ある所から急に乱れてうねり出している。どうやら、この妙な動きに何か秘密がありそうだ。
-
【成島 毅(なるしま たけし)花王株式会社 加工・プロセス開発研究所 研究員。大学では物理学を専攻し、当時のスーパーコンピュータによる計算物理で物性の基礎を研究。1995年、花王(株)に入社。物理・数理科学やシミュレーションを用いて、プロセス技術や製品開発に関わる解析を担当。本稿で紹介するダイレクトエレクトロスピニング(D-ES)技術の開発と化粧品への応用で、他3名とともに 2019年度 繊維学会 技術賞受賞。
マスクの不織布もつくる「エレクトロスピニング」
「実際、吐出された後、乱れたところで繊維の速度は毎秒1~2mでしたが、この繊維の動きは非常に不思議な振る舞いでした。なぜ、どのようなメカニズムで極細化するのか、理論的にきちんとわかっていなかったのです」(成島氏)
実は、繊維の形成技術としては、これは新しいものではない。「エレクトロスピニング」(電界紡糸法)という1900年代初頭から半ばに登場した技術であり、ノズルの中の高分子溶液に高電圧を加えることで極細の繊維ができる。すでに、マスクや衣類素材に使われる不織布(繊維を織らずに絡み合わせたシート)などの製造で実用化されている。
しかしこの繊維は、工場にある、人の背よりも大きな装置の中で紡がれていく。その様子を一般の人が目にすることはなかった。それを手のひらサイズの小型デバイスで可能にし、肌の上にも直接紡糸できるようにしたのが、ダイレクトエレクトロスピニング(D-ES)技術、通称「ファインファイバー技術」というわけだ。

-
図2. 一般的な不織布の例としておむつに使用される繊維(左)とファインファイバー(右)との比較。肌に見立てた人工皮革との接触面を拡大して撮影。ファインファイバー膜の方が、密着性が高く、毛管力により乳液などを浸透・保持することができる。
おかしな動きと「直径サブミクロンの謎」
「それはすごい。(どういうわけだか)極細繊維を紡ぐ装置の小型化に成功したのだ。めでたし、めでたし……」と、ここで片付けてしまうこともできるが、謎を放っておかないのが、花王の研究者だ。
「なぜ繊維がここまで細くなるのか。エレクトロスピニング現象でいったい何が起こっているのか。その本質に迫るべく、数理解析グループでシミュレーションを行いました」(成島氏)
まず、エレクトロスピニングの原理はどうなっているのか。高分子溶液が入ったノズルに電圧をかけると、プラスに帯電した繊維が吐出される。すると、成膜したい表面(基板)との間に電位差が生じ(今回の場合は肌がマイナス極の役割を果たすことで)静電引力で繊維は基板へと引っ張られていく。
この時のノズルの吐出口から基板へ到達するまでの軌道を、点と線で区分して、近似することで、シミュレーションのための「モデル」ができる。打つ点が多いほど、点と点の間隔は狭まり、より正確に近似できる。短い直線をつなぎ合わせて、なめらかな曲線を再現するイメージだ。
-
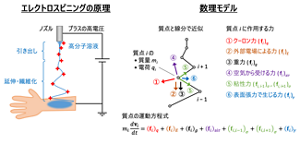
図3. エレクトロスピニングの原理(左)と、この現象を近似して数理モデル化する際に抽出した力の要素(右)。シミュレーションでは物性や条件に、実測値や便覧値を使用して計算が行われた。
「数理モデルに落とし込む際には、各々の質点(先ほどの点に質量を加味したもの)に働くさまざまな力をきちんと取り込むことが重要です。質点はプラスに帯電しているので、質点同士に働く反発力(図3のクーロン力)が生じます。また、ノズルから肌に向かう外部電場からの力も加わります。さらに重力や空気抵抗、溶液の粘性力と表面張力まで、これらすべてを取り込んだ運動方程式を計算機で解くわけです」(成島氏)
モデル化する際に質点を1万個とると、例えばクーロン力の計算はざっと質点数の2乗、 1億回も繰り返することになり、複雑な計算では80時間にも及んだという。果たして、シミュレーション結果からは何が見えたのか。
「麺延ばし」との共通点
「最初の数理モデルでは、ノズルから吐出した直後に回転運動する様子は再現されたのですが、その後の“乱れ”が見られませんでした。そこで、ノズル(出発点)からの距離に対し、繊維の速さと直径がどうなっているのか確認すると、速度は実測に近い値でしたが、直径については7μmと、一桁太い値を示していたのです」(成島氏)
やはり“乱れ”と“細さ”は深く関わっているに違いない。そこで成島氏はモデルを改良した。先のモデルでは、線分は下へいくにつれ、そのまま伸びる設定だったので、線分が長くなってきたら分割し、滑らかな軌跡を描くように変更したのだ。
その結果、小さな回転運動から、無秩序に乱れたカオスな運動へと変化する様子をシミュレーション上で再現することに成功した。繊維の直径も実際の値に格段に近づいた。やはり、細径化の主要因は“乱れること”にあると言えそうだ。
花王 アジュバンドによる葉の濡れ性向上
-
エレクトロスピニングのシミュレーション。
(1) 最初の数理モデル。ノズルから吐出した直後の回転運動は再現されたが、その後の“乱れ”が見られない。
(2) 改良したモデル。線分が長くなったら分割する。小さな回転運動から、無秩序に乱れたカオスな運動へと変化する様子を再現。
(3) 真空条件を想定して図3のモデルから④の空気抵抗を除外すると、“乱れ”が現れなくなる。
では、なぜ乱れると細くなるのか。そこにはエレクトロスピニング特有の不安定さが関係しているという。
「ノズルから出た繊維が少しでも曲がると、電荷の並びにズレが生じます。すると、質点同士の電荷反発力による弾き飛ばすような力で、直進運動は不安定になります。これが“うねり”の原因となって、屈曲していくことで、全体としては乱れた動きを示すと考えられます。うねって屈曲すれば、繊維は長く細くなります。そして、細くなって表面積が増えることで、空気抵抗が増し、滞空時間も長くなり、さらに細径化が進むというサイクルを描いているようです」(成島氏)
-
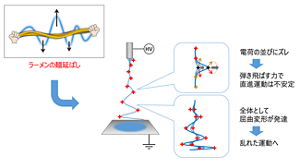
図4. エレクトロスピニングによる細径化の理由は、麺延ばしと同じ屈曲変形にあった(左上は麺延ばしのイメージ図)。
イメージが沸かない人は、ラーメンの麺延ばしを想像するとわかりやすいかもしれない。麺を延ばす際に両端を持つ手と手の間隔が、ノズルと基板の距離に相当する(手をめいっぱい広げ、それ以上は開けない幅で固定して考える)。その幅のなかで、バタバタと乱れさせて、麺を細長くするのが麺打ちなら、同じことを静電反発によるカオスな運動で実現しているのが、エレクトロスピニングと言えるだろう。
数理科学だから、できること
ちなみに、真空中ではほとんど曲がることなく、ほぼ直進することがシミュレーションで示されている(上の動画(3)を参照)。空気抵抗がないと、大きく屈曲する間もなく、あっという間に基板に到達する。細くなるためには時間的な余裕も必要なのだ。真空装置をわざわざ持ち出さなくても、こうした考察が得られるのも、シミュレーションの大きな利点だ。
「もちろん理論がすべてではありませんが、数理解析で現象を理解することで“思い込み”を正すことができます。何に注目すべきかを明らかにして、方向性を示すことに貢献していきたいと考えています」(成島氏)
このようにして数理解析から得られた知見をもとに、現在もファインファイバー技術のさらなる改良が進んでいる。
さて、次回の記事では、数理科学の予測から生まれた「究極の水玉」を紹介。こちら
疑問に真摯に向き合っていく研究員の姿に、あなたもきっと、ものづくりの真髄を見るに違いない。
powered by ブルーバックス
<参考文献一覧>
・成島毅,東城武彦「エレクトロスピニングにおける吐出ポリマー挙動の数理モデリング」 Journal of Textile Engineering 2019, 65, 91-95.
・山下義裕「飛び立つエレクトロスピニングナノファイバー」 繊維学会誌 2020,第76巻 第2号,75-79
・D. H. Reneker et al. Electrospinning jets and polymer nanofibers. Polymer 2008, 49, 2387 -2425
- TOP
- イノベーションのDNA
- 数理科学が暴いた!話題沸騰「ファインファイバー」の秘密






