- TOP
- イノベーションのDNA
- 日用品企業でフラクタル研究?常識を超えた「究極の水玉」が完成するまで
イノベーションのDNA

-
#数理科学 #界面科学 #超撥水
【特集:数理科学】
日用品企業でフラクタル研究?常識を超えた「究極の水玉」が完成するまで
無限の化学に「本質の数理」が挑む(3)
-
2020/08/19 Text by 堀川晃菜

「ファインファイバー」「めぐりズム」「キャラクター泡」。これら “花王の顔”とも言える製品技術の開発には、陰の立役者として数理解析グループの存在があった。
あの大ヒット商品の裏に『数理科学』あり!
数理科学が暴いた!話題沸騰「ファインファイバー」の秘密
これまで紹介した事例は、いずれも物理化学的な現象がまず先にあり、その本質を解き明かすことが数理解析グループの使命だった。研究開発の指針を示す羅針盤のような役割だ。
その一方で、数理には「まったく新しいもの」を生み出す力も秘められている。その実例として、花王の数理科学の研究史に刻まれている「究極の水玉」を紹介しよう。
ノーベル賞学者も認めた「究極の水玉」



-
図1. 数理科学の予測から生まれた究極の水玉(左/上)と、通常の水滴(右/下)。両者の違いについては後述する。
まずは上の水滴の写真を見比べてほしい。何か違和感がないだろうか。
そう、左側の水滴は、まるで絵に描いたように見事な球形、まさしく「水玉」なのだ。もちろん地上で撮影された写真なので、重力の影響は受けている。でも普通、こうはならない。右側のように半球状になるのがよく目にする水滴の姿だ。
実はこの「究極の水玉」の生みの親こそ、花王の数理科学を長年リードしてきた恩田智彦氏だ。
時は27年前。1993年にさかのぼる。この頃、物理や数学を専門とする人たちの間では「フラクタル」と呼ばれる特殊な形が話題になっていた。
「私が中途で花王に入社してすぐの頃です。社内でもフラクタル表面というのは、水にぬれるのか、ぬれないのか? という議論が巻き起こっていました。そこで、この疑問に答えてみたいと思ったのです」(恩田氏)
-
【恩田 智彦(おんだ ともひろ)花王株式会社 研究開発部門 シニアパートナー。工学博士。東京大学工学部助手を経て1992年 花王(株)に入社。物理・数理科学の視点から各研究所の商品開発で現れた新たな物理・化学現象を理論的に解明し、開発指針の提言や最適物性・構造の予測を行う。界面科学、レオロジー(流動学)、相変化型光ディスク、内臓脂肪計の研究開発に従事。
自然界の神秘?「フラクタル」
ざっくり言うと、フラクタルとは、自分の中に自分と似た(より小さな・または大きな)形をもった構造で、「自己相似性を持つ」という特徴がある。
-
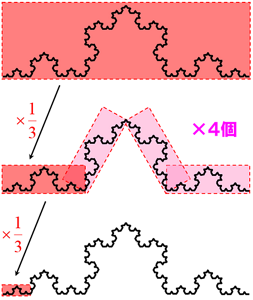
図2. フラクタルの例(コッホ曲線)。全体を「3分の1」に縮小したミニチュアの自分が、元の自分の中に「4個」含まれるという関係が延々と続いていく。
さらに、フラクタルには「小数の次元」で表されるという特徴もある。たとえば、図2のコッホ曲線は約1.26次元だ。詳細については数学の参考書に譲らせもらうが、1と2と3の間の次元が出てくる……という心の準備だけしてもらえたらと思う。
さっそく頭がこんがらがってきた人も、ひとまず身近にあるフラクタルをご覧いただきたい。下の写真はカリフラワーの仲間であるロマネスコという野菜だ。他にも、リアス式海岸の地形、入道雲の表面もフラクタルだ。さらに人体の中にも、その構造を見ることができる。血管は大動脈から毛細血管に至るまで分岐を繰り返す。肺では、多くの肺胞に空気を行き渡らせるため、気管支が分岐している。これもフラクタルだ。

-
図3. フラクタル構造を持った野菜。ロマネスコ
ロマネスコの写真からもわかるが、フラクタルはものすごく凸凹している。このため、長さあるいは表面積が莫大になるという性質がある。90年代当時から、世の中ではこの性質を生かした応用の可能性が活発に議論されていた。
「たとえば、活性炭はフラクタルの1つで、広い表面積でにおい物質を吸着することで脱臭効果につなげているわけですが、我々が扱う商品では、さまざまな場面で“濡れ”というものが重要になります。つまり、固体の表面が液体をはじくか、あるいは濡らすかという性質です。この“濡れ”の分野にフラクタル表面を応用できないか、と目を付けました」(恩田氏)
結論から先に言ってしまうと、先ほど示した「究極の水玉」は、フラクタル表面に乗せた水滴なのだ(他方、半球状の水滴は平らな表面に乗せたもの)。これは、フラクタル表面では超撥水現象が起きることを理論的に予測し、実証に成功したものだ。しかし、周囲はもちろん恩田氏自身も当初「本当にそんなことが起きるだろうか」と半信半疑だったという。
ひらめきの瞬間が訪れる
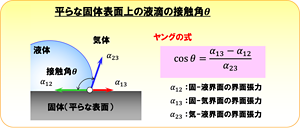
液体をはじくのか、それとも濡らすのか。「濡れ」を考える際には、物体(固体)・水(液体)・空気(気体)の3者の境界面に注目する。図4の緑、赤、青色の矢印で示すように、各々の界面には界面張力が働いている。この3つの界面張力の引っ張り合うバランスによって、水滴が潰れるか、コロンとした球形に近づくかが決まる。それを数式で表したのが「ヤングの式」だ。
-
図4. 平らな面における界面張力と接触角の関係を示すヤングの式。接触角θが大きくなるほど、水滴は球形に近づき、固体表面からはじかれる。θが小さくなるほど水滴は潰れて、固体表面をぬらす。
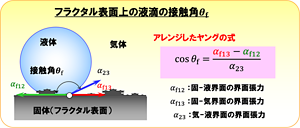
ただし、このヤングの式は平らな面において成立する。そこで恩田氏は、この固体表面の界面張力(固体‐液体の界面:緑色の矢印、固体‐気体の界面:赤色の矢印)を微細な凹凸構造をもつフラクタル表面の(みかけの)界面張力に置き換えることで、ヤングの式をアレンジすることを思いついた(図5)。
-
図5. フラクタル表面に適用するために恩田氏が考案したヤングの式のアレンジ
無限大? フラクタルの表面積を見積もるには
では、フラクタル表面における界面張力は、どうやって求めればよいのか。
「平らな面の界面張力は、単位面積1㎠ の断片に蓄えられている界面エネルギーと捉えることができます。フラクタル表面の場合は、1㎠の断片の中に莫大な表面積が存在しているので、界面エネルギーもたくさん蓄えていることになります。ならば、この表面積が何倍になっているのか、その倍率を計算式に反映すればフラクタル表面の界面張力を見積もれると考えました」(恩田氏)
この倍率をここでは「フラクタル表面の粗さ因子」と呼ぶことにする。くしゃくしゃにした紙を引き延ばすように、仮にフラクタル構造を真っ平に延ばしたらどうなるか、という視点で次の図を眺めてほしい。延ばせた倍率が「粗さ因子」だ。
-
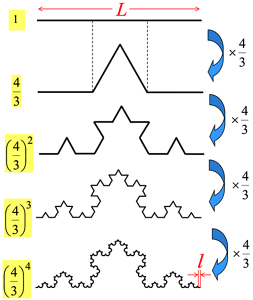
図6. フラクタル表面の「粗さ因子」の算出(コッホ曲線を例に)
簡単のため、コッホ曲線で考えてみる。図6を上から追ってみてほしい。まず、1本の線分を3等分して、真ん中の線分を山型の2本の線分に置きかえる。この操作を繰り返すことによってコッホ曲線が得られる。1回の操作で線全体の長さは4/3倍になるから、この操作をn回繰り返して得られるコッホ曲線の粗さ因子は4/3のn乗になる(操作を無限回、繰り返すと「粗さ因子」は無限大になる )。
恩田氏はこの考え方を一般のフラクタル表面に拡張した。そして、フラクタル表面の「粗さ因子」が(L/l)D-2 で表されることを導いた。ここでLは最初に用意した長い線分の長さ、lは等分を繰り返していって短くなった線分の長さである。そして、Dは次元を表している。この場合、Dの値は2と3の間の小数になる。面(2次元)と体積(3次元)の間の次元をもつのだ。
数式は何を語ったか
そして、導き出した「粗さ因子」をアレンジしたヤングの式に適用して、最終的に恩田氏が導いたのが次に示す式だ。
-
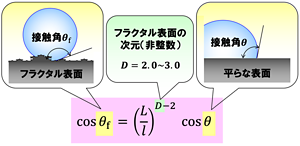
図7. フラクタル表面の接触角と平らな面の接触角の関係式
cosθf = (L/l)D-2 cosθ
これを言葉で表してみる。
〔フラクタル表面の接触角のコサイン〕=〔フラクタル表面の粗さ因子〕×〔通常の平らな面での接触角のコサイン〕
高校数学に出てくる三角関数の知識だが、θが90度以下ではcosθは正の値に、90度以上だと負の値になる。一方で、フラクタル表面は莫大な表面積を有しているので粗さ因子(L/l)D-2は非常に大きい(たとえばL=100μm、l=1μm、D=2.5のとき(L/l)D-2=10となる)。
こうして上式の右辺は、正の値(θが90度以下)に大きな値を掛けてより大きなプラスになったり、負の値(θが90度以上)に大きな値を掛けてより大きなマイナスになったりする。左辺にある「フラクタル表面の接触角θfのコサイン」はそんな極端な値をとるのだ。
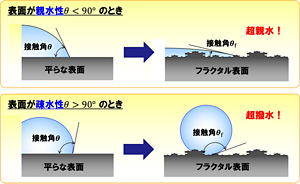
つまり、この式は「フラクタル表面はものすごく水に濡れるか、ものすごく水をはじくか」という対極的な2つの性質をもつことを示している。親水性の素材でできたフラクタル表面では、接触角θfは0に近づいて「超親水」になり、疎水性素材のフラクタル表面では接触角θfが180°に近づいて「超撥水」になるはずだ(図8)。
-
図8.フラクタル表面の濡れの予測結果。フラクタル表面には微細な凹凸があって表面積が大きいため濡れが強調される結果、超撥水や超親水現象が現れる。固体が疎水性の場合は、水滴はフラクタル表面との接触をなるべく避けようとして、体積を一定にしたまま1番表面積を小さくできる球形におさまる。反対に、固体が親水性の場合は、水滴はフラクタル表面になるべく触れようとして表面上をぬれ広がる。
私たちはすでに「究極の水玉」を見た後なので、そう聞いても驚かないかもしれない。しかし、当時の恩田氏にとっては、自らが導いた式の意味することは、誰も見たことのない現象であり、半信半疑だった。周りにもほとんど信じてもらえなかったという。
ただ一人「信じてみよう」と言ってくれたのが、当時の基礎科学研究所の辻井薫所長だった。そして、現在ヘアケア研究所の四分一敬氏が実験をした結果、見事に撮影されたのが、あの「究極の水玉」というわけだ。
数理の「予言」は的中した
恩田氏は実験成功の知らせを同僚の結婚式の場で受けた。あまりの感激でご祝儀袋を渡し忘れそうになったそうだ。これぞまさに「数理の予言」が証明された瞬間だった。
その後、花王にノーベル賞物理学者(1991年受賞)でフランス人のピエール=ジル・ドゥジェンヌ氏が来社した際には、その成果に感嘆の声をあげたという。ドゥジェンヌ氏の著書(『表面張力の物理学─しずく、あわ、みずたま、さざなみの世界─』吉岡書店)にも、この内容が記されている。
そして、気になるその後の応用について、恩田氏は次のように語った。
「色々な分野から引き合いがきたのですが、表面汚染や強度の問題で、フラクタル表面の超撥水状態を長時間維持することが難しく、残念ながら当時、実用化に結び付けることはできませんでした。それでも、日用品では水や油をはじいたり、濡らしたりする“濡れ”現象が頻繁に現れます。今でもさまざまな場面で、固体表面に微細な凹凸を付与して“濡れ”を制御するという考え方が生かされています」
約30年前、経営陣のトップダウンで始まった花王の数理研究。はじめのうちは「難しいことをやっている人たち」と言われたが、その歩みを止めることはなかった。あらゆる自然現象を相手にできる数理科学の最大の強みを生かし、着実に実績を重ねていった。今では数理解析グループの研究メンバーからのボトムアップによって数理解析研究が社内に浸透している。
役に立つかどうかは、やってみないと分からない。すぐには形にならないかもしれない。それでも、誰かが新しい扉を開いてく。だから私たちは明日に可能性を感じられるのだろう。こうして「イノベーションのDNA」は未来へと受け継がれていく。
【これまでの記事】
1本目の記事:あの大ヒット商品の裏に『数理科学』あり!
2本目の記事:数理科学が暴いた!話題沸騰「ファインファイバー」の秘密
powered by ブルーバックス
<参考文献一覧>
・恩田智彦, 塩見浩之「製品の中の界面現象の数理」 応用数理 2018, 28, 71-75.
・恩田智彦「フラクタル表面構造と親水性・撥水性の物理」 J. Vac. Soc. Jpn. 2015, 58, 424-430.
・Onda, T., Shibuichi, S., Satoh, N. and Tsujii, K., Super-water-repellent fractal surfaces. Langmuir 1996, 12, 2125-2127.

- TOP
- イノベーションのDNA
- 日用品企業でフラクタル研究?常識を超えた「究極の水玉」が完成するまで






