- TOP
- イノベーションのDNA
- あの大ヒット商品の裏に『数理科学』あり!無限の化学に「本質の数理」が挑む
イノベーションのDNA

-
#数理科学 #界面科学 #創る/シミュレーション #蒸気温熱シート #泡スタンプ
【特集:数理科学】
あの大ヒット商品の裏に『数理科学』あり!
無限の化学に「本質の数理」が挑む(1)
-
2020/08/05 Text by 堀川晃菜

「ターニングポイントは、ありません」
数理科学が専門の恩田智彦氏が花王へ中途入社したのは、今から約30年前の1992年。まだほとんどの人がインターネットを知らなかった時代のことだ。
大学で助手をしていた恩田氏がたどり着いた、そこはまさに「化学の城」。花王の研究開発部門は化学系、生物系の研究員が大多数を占め、現在も数理科学を専門とする人は研究員全体の1パーセントに満たない。
その中で恩田氏は、数理解析グループの元グループリーダー(現在はシニアパートナー)として、数理科学をものづくりへ生かす道を模索してきた。
「私たちは直接ものづくりをするわけではないので、数理が何の役に立つのかと言われることもありました。逆に、何でも計算できると思われて困ったこともありましたね」と恩田氏は振り返る。
数理科学に対する疑心と過信を払拭し、「正しい信頼」を獲得するまでの道のりは、地道に歩むしかなかった。それを表しているのが冒頭の言葉だ。一つひとつの仕事を丁寧に仕上げ、それを積み重ねてきたことで、数理科学が活躍する機会も増えてきたという。
今ではヒット商品の開発を強力にサポートした事例も一つや二つではない。では実際、どのようにして、ものづくりの現場に寄与してきたのだろうか。
恩田 智彦(おんだ ともひろ)花王株式会社 研究開発部門 シニアパートナー。工学博士。東京大学工学部助手を経て1992年 花王(株)に入社。物理・数理科学の視点から各研究所の商品開発で現れた新たな物理・化学現象を理論的に解明し、開発指針の提言や最適物性・構造の予測を行う。界面科学、レオロジー(流動学)、相変化型光ディスク、内臓脂肪計の研究開発に従事
「数理科学」で何をするのか
数理科学とは、世の中の現象を数学というツールによって理解・予測しようとする学問だ※。
私たちが学校で算数や数学を習うときは、まず解き方を教わる。与えられた式が解けるようになると、今度は与えられた課題を解く。例えば文章問題では、数字を拾いながら自分で式を立てる。その式でうまく答えが出せなければ、また式を立て直すところからやり直す。
数理科学は、これを実社会のレベルで行っていると言えるだろう。「課題」はあらゆるところから生じる。化学反応や物理現象といった自然現象を相手にすることもあれば、交通渋滞だったり、金融市場だったり、人の関わる社会現象を対象とした研究もある。
だが現実の世界は、いくつもの要素が複雑に絡み合っている。複雑怪奇にみえる現象から本質を見抜くことが何より重要になる。「モデル化」と呼ばれるプロセスだ。
「なにが幹で、どこが枝葉なのか。それをまず見極めることが数理モデルに落とし込む上で一番大切なことです」(恩田氏)
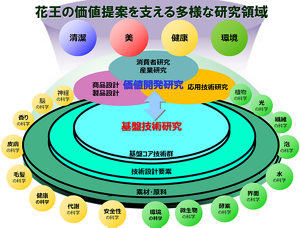
多種多様な商品を手掛ける花王は、研究領域も「衛生」「美」「健康」「環境」と幅広い。そして、数理科学はこれらの研究開発を横断的に支えている。解析対象とする自然現象も、界面現象、光学現象、流体現象、力学現象とさまざまだ。
例えば、化粧品用のクリームやオイルを肌になじみやすくするのは界面現象が、パウダーファンデーションや口紅のパール材の輝きには光学現象が関係している。また、液体製品などを製造するタンク内の攪拌・混合過程には流体現象が、ボトルの強度の設計などには力学現象が関わっている。
そのなかでも特に「数理の力を実感した」と恩田氏が語るのが「めぐりズム」の開発エピソードだ。
-
図1. 花王の研究領域
「めぐりズム」誕生の舞台裏
目元を温めてくれるホットアイマスクを使ったことのある人も多いのではないだろうか。蒸気でシート全体がじんわりと温まる「めぐりズム」シリーズ。アツアツのおしぼりが少し冷めてきたぐらいの、最適な温度がなんとも心地よい。
だが、これを実現するために欠かせないのが、シート全体に鉄粉をまんべんなく仕込むことだ。このシートの熱源は、鉄と水分と空気中の酸素の化学反応によって生じる熱。だからもし、シート中の鉄粉に偏りがあると、温かさにムラが出てしまう。
つまり鉄粉の均一分布は、この商品の肝だ。しかし、それがまた最大の難関でもあった。
初代のめぐりズムは、製紙会社に委託し、紙すきの技術で作られていた。下に示すのは、その装置の構造と原料の流れをシミュレーションした図だ。下から原料(水とパルプが混ざったドロドロの懸濁液)を流し入れると、上の面で塗り広がり、ここで紙すきが行われることになる。



-
図2. 第一世代「めぐりズム」の製造に用いた紙すき法の装置図。
紙の厚みを均一にするため、下から流し込んだ原料が上の面に到達する直前には、原料を堰(せき)に通し、さらに「邪魔板」(じゃまいた)と呼ばれる板にぶつけることで、かき混ぜている。
通常は、紙すき職人が堰の高さや、邪魔板の位置や角度を調整することで、混ざり方に偏りのない均一な紙にしている。しかし、この職人さんの経験をもってしても敵わなかったのが、めぐりズムの鉄粉入り原料だった。
「紙に鉄粉を入れるなど、製紙業界ではまずありえない話ですから、無理もありません。改良前の状態をシミュレーションすると(図2・左/上)中央の赤い部分は原料の流れ方が速く、端にいくほど青くなり、速度が遅くなることを示しています。そうすると、重い鉄粉は中央に押し流されて集まり、両端では少なくなってしまうのです。また、わずかなゆらぎをきっかけに流れが変動し、鉄粉の分布が一定しませんでした」(恩田氏)
なんとか鉄粉の偏りを解消できないか。現場の担当者から相談を持ちかけられたのが数理解析グループの中島武士氏だった。当然ながら紙すきに関しては素人。
ところが、流体シミュレーションにより、堰と邪魔板の設計を最適化した装置を現場に持って行ったところ、わずか1、2回の調整で、鉄粉入りの原料を均一に流すことに成功。見事、製品化にこぎ着けることができた。


-
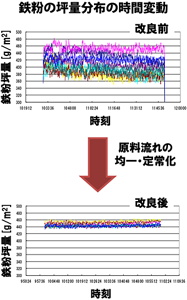
図3. 鉄粉の坪量分布の時間変動。横軸は時間、縦軸は鉄粉の坪量(坪量〔g/m²〕とは板紙1m²当たりの重量を指す)。シートの幅方向に等間隔で並べた8台のセンサーの計測値を8色の線で表した。改良前(左/上)は全体的にばらつきが大きいが、改良後(右/下)では、ほぼ同一線上に数値がのっていることから、シート全体に均一に鉄粉が分布していることがわかる。
だが実は、このシミュレーション結果を出すには、もう一つ不可欠だった要素がある。品質工学の理論だ。
いくら計算上の試行錯誤とはいえ、堰や邪魔板の形状、それぞれの高さや角度、両者の位置など、一つひとつの条件を組み合わせると、膨大なパターンが生じる。その中から最適解を見出すには、シミュレーションを何度も繰り返す必要があり、闇雲にやるわけにはいかない。
ところが、品質工学の理論を用いれば、何百、何千ものパターンを試さなくても、たったの“18通り”で最適解を導き出せるという。この品質工学の力が大いに発揮されたのが、次に紹介する「キャラクター泡」の設計だ。
どうやって? 泡がキャラクターに大変身!
新型コロナウイルスの出現で、手洗いの重要性がますます認識されるようになった。しかし、なかなか大変なのが小さな子どもの手洗いだ。そんなとき、ポンと手のひらにお花の形の泡がのったら。ハート形や、人気のキャラクターの形だったら。大人だって、微笑んでしまう!

これぞ日常を彩る小さな幸せ。手洗いがアミューズメントになるのだ。そして、数理解析グループの坂本雅基氏が2015年に挑んだミッションというのが「泡を癒し系キャラクターに変えるノズルの設計」だった。
ノズルの穴(泡の吐出口)をどのような形状にすれば、思い通りの泡がつくれるか。例えば、泡をハートの形にしたければ、やっぱり穴もハート型かと思いきや……。
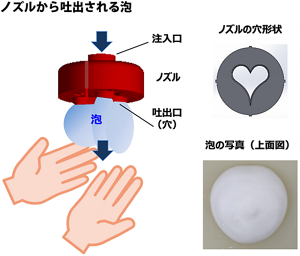

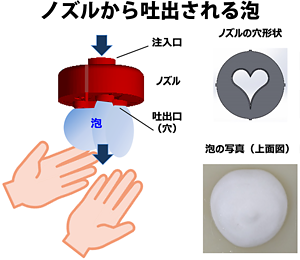
-
図4. ハンドソープのボトル(ディスペンサー)ではノズルの吐出口によって、出てくる泡の形状が変わる
残念ながら、図4(右下の写真)に見るようにハートとは程遠い結果に。ならばと、しらみつぶしにノズルの形を変えていくのも一つの手だが、「泡」というのはちょっと厄介な相手で、その動きを読むのは容易でないという。
つまりシミュレーションで形状予測するにしても、まずハンドソープの泡の“素性”がわからないことには始まらないのだ。
「泡はとても複雑な流体です。液体が流れる時の性質『粘性』と、固体が変形する時の性質『弾性』を合わせ持つ、中間的な性質があります。これを『粘弾性』と言います」(恩田氏)
まず「粘性」と「弾性」について、簡単にイメージを共有しておきたい。「粘性」は、液体の流れやすさを表す性質で、粘度(粘り具合)で示される。あくまでイメージだが、粘度が低いものは、真水のようにサラサラで、粘度が高いものは、蜂蜜のようにドロドロしている。
一方で、「弾性」は固体の変形のしやすさを表す性質だ。その度合いは、弾性率として示される。これはバネを思い浮かべるとわかりやすい。力が加われば固体は変形するが、弾性率が高いほど変形を元に戻そうとする力(弾力)が大きく、固体は硬い。低いほど弾力が小さく、柔らかい。
そして「粘弾性」とは、「粘性」と「弾性」が共存している状態を指している。泡もそうだ。手のひらにのせた洗顔フォームの濃密な泡は固体のように形を維持し、そっと顔を触れるとバネのように押し返してくる。これが弾性だ。一方で、ごしごし顔を洗いだすと泡は顔と手の間で液体のように滑らかに流れる。サラサラとドロドロの中間の粘性を示すのだ。
つまり、泡を理解するには、粘性だけでも、弾性だけでもダメで、両方を調べて「粘弾性」として評価する必要がある。
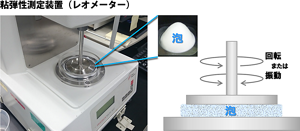
そこで登場するのが、粘弾性を測定するレオメーターという装置だ(図5)。2枚の円盤の間に泡を挟み、回転運動や周期的な振動(往復運動)を加えた際に、粘性や弾性がどのように変化するのか測定することができる。その結果、得られたのが図6に示す2つのグラフだ。


-
図5.粘弾性測定装置(Anton Paar社製、MCR300)。一方向に回転させた際の粘度(回転運動に対する非線形粘度)、往復するように振動させた際の弾性率(周期振動に対する複素弾性率)を測定。

-
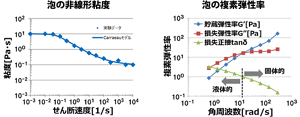
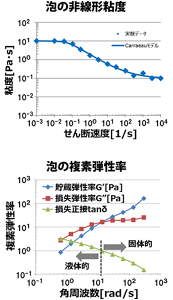
図6 泡の非線形粘度:回転時の速度(せん断速度)と粘度の関係。 泡の複素弾性率:振動の速さ(角周波数)と弾性率の関係。
図6“泡の非線形粘度“は回転が速くなると、泡の粘度は低下し、サラサラになることを示している。一方、図6“泡の複素弾性率“では、青い線が泡の弾性的性質の大きさを、赤い線が泡の粘性的性質の大きさを表し、青と赤の線がクロスする周波数を境に泡の性質が変わる。
つまり、振動がゆっくりのときは粘性的性質の方が大きいから泡は液体のようにふるまい(流動し)、振動が速いときは弾性的性質の方が大きくなって固体のようにふるまう(弾力を示す)。
粘弾性の他にも、密度や表面張力など基礎データを集め、泡の特性を把握したことで、適用すべき流体モデルと入力する物性値に見極めがついた。これでようやく、シミュレーションによる解析・予測が可能となり、コンピューター上で泡の動きが再現された。
花王 キャラクター泡の形状シミュレーション
-
図7. シミュレーションで再現された泡の動き
……しかし、喜ぶのはまだ早かった。
品質工学でシミュレーションを効率化
「ノズルを製作して実際に試さなくても、シミュレーションでその穴からどのような泡ができるか予測できるようにはなりました。それでも、特定のキャラクターの形を最もよく再現する穴の形状を割り出すには、無数の計算を繰り返さなければいけません」(恩田氏)
そう、ここで登場するのが品質工学だ(お待たせしました!)。ではなぜ、条件を探し出す作業を効率化することができるのか。
「品質工学で活用されている直交表※の性質を用いると、3つの水準をもつ7個の設計因子と2つの水準をもつ1個の設計因子の組合せ(3の7乗×2=4374個)の中から特別な18通りを選ぶことができ、その18通りのシミュレーション結果から、最適な条件を予測することができます」(恩田氏)
こうして、シミュレーションと品質工学の合わせ技で、ノズル出口のデザインは大きく前進した。ハートの泡も、文句なしのハート形だ(図8(右))。
花王 キャラクター泡のノズル設計
-
図8. キャラクター泡(ハート形)の設計事例。(左)当初の失敗例。(右)最終的な成功例。
こうして最短距離で“コツ”を掴めたことで、それ以降は必ずしもシミュレーションしなくとも理想の形を作れるようになったという。お花型や人気キャラクターなど、いくつか商品化しているが、泡は丸まろうとするため、尖った形やくびれのある形は難易度が高いそうだ。
さて、今回は流体シミュレーションの応用事例を2つ紹介した。こうして成功事例を並べると、はじめからすんなりと数理科学が受け入れられ、うまくいったように見えるかもしれない。しかし数理科学が市民権を得たのは、恩田氏が約30年携わってきたなかで、ここ10~15年の話だ。
徐々に解析を依頼されるケースも増え、最近では“未来の肌”として注目を集める「ファインファイバーテクノロジー」の開発にもその知見が生かされている。一方では、花王の数理科学研究が、学術的にも大きなインパクトをもたらしたこともある。
続く2本目の記事では、ファインファイバー技術における数理科学の最新の応用事例に迫る。こちら
さらに最終回3本目の記事で、数理科学の予測から生まれ、ノーベル賞学者も唸らせた「究極の水玉」を紹介。こちら
powered by ブルーバックス
※主な参照先
●数理科学について
・数理科学する、って何? 教えて、めいじろう(明治大学)
・ものづくり企業に役立つ応用数理手法の研究会(日本応用数理学会)
●品質工学については関西品質工学研究会の以下のページが参考になる
・「品質工学」については、こちら
・「直交表」については、こちら
※参考文献
●商品開発における数理科学(応用数理)の役割
恩田智彦, 塩見浩之「製品の中の界面現象の数理」 応用数理 2018, 28, 71-75.
●発熱シートの開発及び製造装置のデザインについて
熊本吉晃,石川雅隆,宇賀神徹,河尻浩宣「抄紙法を用いた機能性発熱シートの開発」 繊維と工業,2007, 63, 292-295.
中島武士「シミュレーションによる抄紙型発熱体の坪量分布均一化」 第16 回品質工学研究発表大会,2008, 16, 346-349.
●「キャラクター泡」および品質工学について
高城栄政「手のひらに載せて、眺めていたくなる“泡”を」 The Invention, 2018年7月号, pp.5-11.
坂本雅基「洗剤スラリーの流動性向上に関する検討」 品質工学,2003, 11, 77-84.
坂本雅基「流体シミュレーションを用いた粉体化粧料の分散性向上に関する検討」
第24 回品質工学研究発表会,2016, 24, 14-17.
- TOP
- イノベーションのDNA
- あの大ヒット商品の裏に『数理科学』あり!無限の化学に「本質の数理」が挑む






